1 いろいろな関数 12 関数とグラフ 関数 x に対して唯一つy が決まるとき,この対応を関数という. y = f(x) と書く事が多い. 定義域 関数y = f(x) で,x の動く範囲. D などで表す. 値域 関数y = f(x) で,定義域内のx に対応するy の動く範囲. 定義域D に対してf(D) と書く. 例11 y = 1=x を0 < x < 1微分(総合) いろいろな関数の導関数 (関数の組合せ)・・・問題数が多いので,必ずしも全部を解く必要はありません。 「ある範囲までは習っているが他の範囲は習っていない」というような場合に,範囲を制限した問題練習が可能です。 計算用紙は必要です・・・現役生徒が手ぶらで解くのは無理でしょう。 以下の関数は,定義可能かつ微分可能な範囲でのみ35 いろいろな関数のグラフ p46 第2次導関数と曲線の凹凸 漸近線 分数関数のグラフ 無理関数のグラフ 三角関数のグラフ 指数関数のグラフ 対数関数のグラフ 対称性 36 物理的思考 p55 1次元の運動 2次元の運動 さまざまな量の変化率 37 近似式 p57 1次式近似

指数関数ものがたり 西郷 甲矢人 能美 十三 本 通販 Amazon
いろいろ な 関数
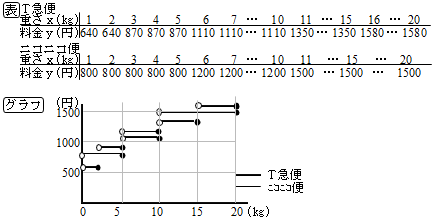
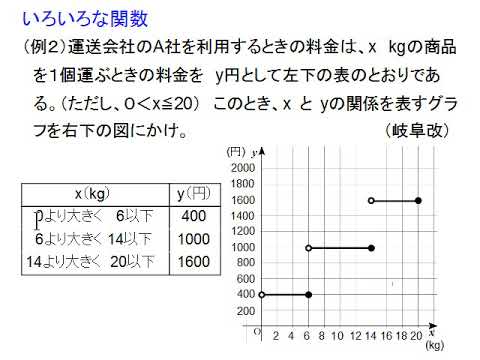
いろいろ な 関数-いろいろな曲線の確認 ★いろいろな曲線の代表的なものを確認しておこう。 余擺 よはい 線 せん とも。半径a の円がx 軸上を滑らずに転がると き、円の周上の定点P の描く曲線。エピトコロイド、ハ イポトコロイドも各サイクロイドのものにつながる。 sin③ は の関数といえるか、いえないか。 右のグラフは、重さ gの 荷物の配送料金を 円として、 と の関係を表したもの である。 グラフで端の点をふくむ場合は「 」 ふくまない場合は 「 」で表している。




中学数学で登場する不連続な関数 身勝手な主張
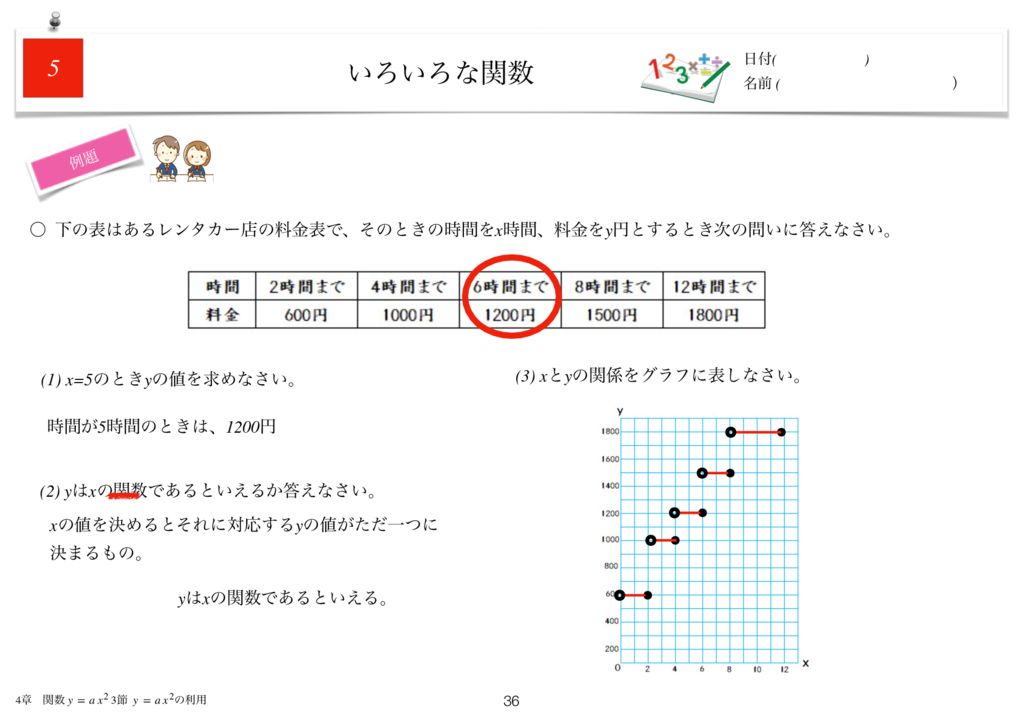
よって,奇関数でも偶関数でもない. £ ¢ ⁄ ¡ 問2 (1) この関数のグラフは,y = x3 のグラフをx 軸方向に ¡2,y 軸方向に1 平行移動したものである. また,x = 0 のとき y = (02)3 1 = 81 = 9 ¡2 1 9 x y O (2) この関数のグラフは,y = ¡x3 のグラフをx 軸方向いろいろ ろな関数 (本時) グラフが階段状になる関数について、値の変化を調べたり、同様の関数と値を な関数 比較し考察したりすること 章の問題A 第 時12 2 y = a χ いろいろな関数 数量の関係を1つの式で表せなく、定義域を分けて、各定義域ごとの関数を考える問題です。 ガウス関数という高校数学で詳しく学びますが、中学では郵便物や駐車場の料金などのグラフの問題が出題されます。 具体的な問題でグラフを
高校講座HOME >> ライブラリーTOP >> 数学Ⅱ 数学Ⅱ 出演者紹介 年度に放送した「NHK高校講座」の再放送です。 全科目・全回を各1回、年10いろいろな 関数 ~グラフを 利用 して 解決 しよう ~ <教材観 > 高等学校 の数学 においては 、1次関数 、2次関数 を始めとして 様々な関数 を学習 する 。そこ ではグラフで 表現 することが 非常 に有効Countif関数 の基本的な 私、最近社内で「エクセルの関数ができる」と思われて、いろいろな業務が回ってくるんですよ。上司から「どの地域に人気があるか、簡単に集計できないか?」といわれ、「人気旅行先ベスト
いろいろな2次方程式~ ホップ ステップ ジャンプ 9 2次方程式(3) ~2次方程式の利用~ ホップ ステップ ジャンプ 10 関数y=ax 2 (1) ~関数y max関数は、指定した範囲内の数値の最大値を求める関数です。 = の後に MAX と入力し、その後の引数部分には (範囲内の最初のセル最後のセル) を入力します。 xの関数であるyの具体例を紹介しよう。 中学1年生では、 y = 2 x のようなシンプルな関数が登場するよ。 この関数のxに数字の「2」を入れてあげるとyの値は「4」になるし、 xに「3」を入れると、yは「6」になるね。 xに何をぶち込むかによって、yの値がちがう。



いろいろな関数の導関数 微分




いろいろな関数の導関数 の勉強法のわからないを5分で解決 映像授業のtry It トライイット
いろいろな三角関数 関数 y = sin ( θ − π 3 ) {\displaystyle y=\sin \left(\theta {\frac {\pi }{3}}\right)} のグラフは、 y = sin θ {\displaystyle y=\sin \theta } のグラフを θ軸方向に π 3 {\displaystyle {\frac {\pi }{3}}} だけ平行移動させたものになり、周期は 2 π {\displaystyle 2\pi } である。高校数学の基本問題 Gogle site →数ⅠA →数ⅡB →数Ⅲ (旧C) ***最近の更新*** 反復試行の確率(入試問題) 絶対値付き関数の定積分 Rの関数hist () Rの関数sample () 名義尺度データの比率の検定 フィッシャーの正確導関数の計算で高校数学を総復習 「いろいろな関数の導関数を定義に従って計算する」ことで高校数学のいろいろな分野の復習ができます。 例えば, x n x^n x n の微分は 二項定理 , 1 x \dfrac{1}{x} x 1 の微分は 分数式の計算 , x \sqrt{x} x の微分は 有理化 ,



授業実践記録 数学 関数の考えを用いて主体的に問題を解決しようとする態度を育てる学習指導 啓林館
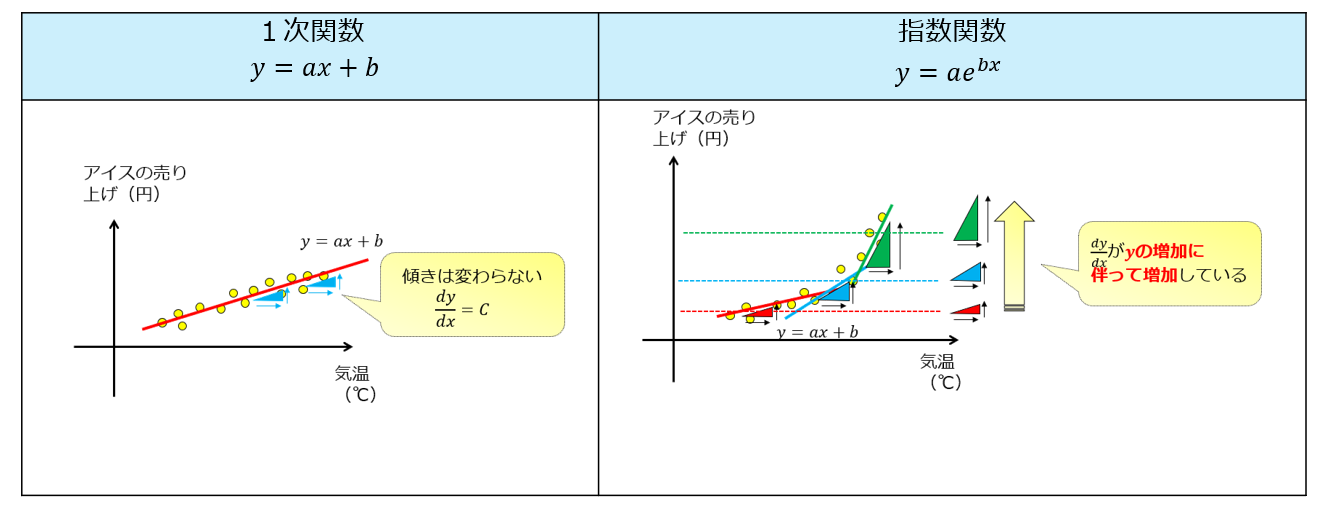



指数関数の意味 高校生からわかる近似曲線に指数関数を選ぶとき 宇宙に入ったカマキリ
(1) ガウシアンのフーリエ変換はガウシアン ここで定積分 は次のように 2 次元平面上の積分を使って求められる (2) 指数関数のフーリエ変換はローレンツィアン (3) 正弦波のフーリエ変換はデルタ関数 これは、正弦波が直交基底であるという意味なので天下り的に認める。単元 関数 y = a x 2 (啓林館) 3 いろいろな事象と関数 ・2・ いろいろな関数 全1時間分数関数について 反比例のグラフ、分数関数のグラフを描画します。 上手に式を考えると、面白いグラフがいろいろ描けます。数学の教科書や参考書を見ていろいろ試すのも面白いと思います。 例えばこんな式(4つすべて描いてください)。 y=(xx)/(x5) y




数学 いろいろな関数の導関数 Youtube




1次不等式 いろいろな関数の問題です F1 数学 箱根駅伝ブログ
いろいろな関数の微分の説明 に使われています。数学Ⅲの微分積分のテーマは 今まで習った関数の全てを微分(積分)できるようにする ことです。つまり「新しいことがほとんど」 というわけではない ということですね。 もちろん新しいことも出てきメビウス関数 : n が 平方因子 を持つ数ならば μ ( n) = 0、 n が相異なる 偶数 個の素数の積ならば μ ( n) = 1、 n が相異なる 奇数 個の素数の積ならば μ ( n) = −1 と n によって3通りの値をとる関数。 ゼータ関数 およびその類似物である L関数 :これらの関数と素数の間に深い関係があることは、 リーマン予想 で示唆されている。 リーマン予想 を仮定するといろいろな曲線を方程式の形に表す場合、Y=F(X) のような陽関数だけでは表現しきれ ない。 媒介変数表示の方法は万能ではあるが、式自体に美しさが感じられない。



function view問題集 ver3 42j



指数法則の一覧 統計学でよく使うもの 統計学が わかった
カーネル関数は他にもいろいろな手法にも使えます。変数間の非線形性を考慮するための便利な関数です。カーネル関数、最高! たとえば svm では、次のような文脈でカーネル関数が出てきます。 線形の svm モデルを定式化できた (式で表せた)! ↓ f (x) f (x) が三次以下の関数のとき, ∫ a b f ( x) d x = ( b − a) 6 { f ( a) 4 f ( a b 2) f ( b) } \displaystyle\int_a^bf (x)dx=\dfrac { (ba)} {6}\ {f (a)4f (\dfrac {ab} {2})f (b)\} ∫ ab f (x)dx = 6(b− a) {f (a)4f ( 2a b )f (b)}Share your videos with friends, family, and the world




いろいろな関数 中3数学 関数y Ax二乗 11 Youtube




中学数学で登場する不連続な関数 身勝手な主張
エクセルのor関数の使い方を図と例で理解する 16年4月21日 エクセルのor関数は、入力された論理式に応じて次のような値を返す関数です。 区分 返り値 ひとつでも 「true(真)」の場合 「true(真)」 すべて 「false(偽)」の場合 「false(偽)」香川亮の数学基本大全 数Ⅲ いろいろな関数 数学Ⅲ2a 分数関数(2) 方程式と不等式 いろいろな関数




1 Y Log2x 3 Log2x3 0x Descubre Como Resolverlo En Qanda
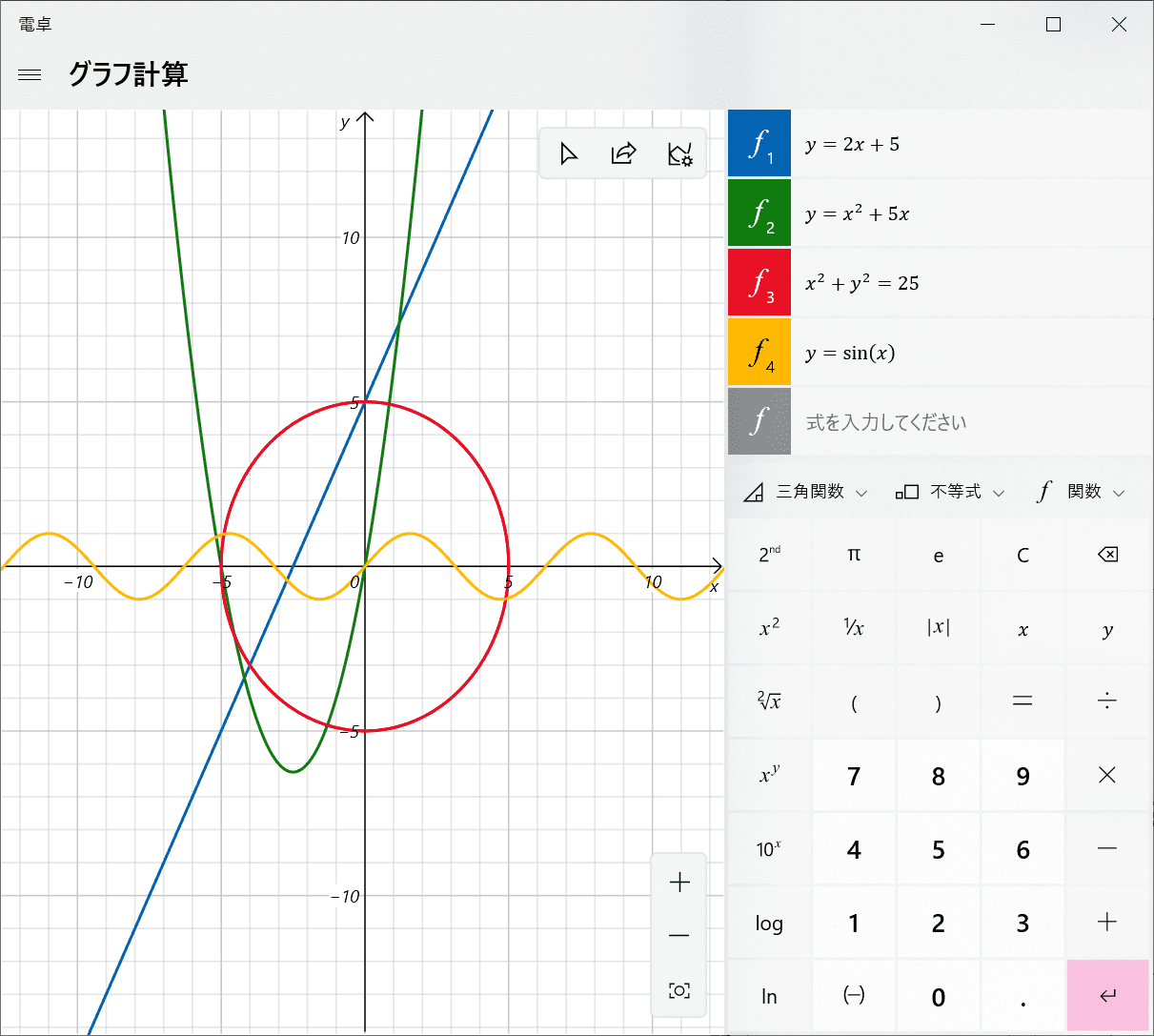



高校数学の関数グラフをwindows10の電卓で描く 志木駅前のパソコン教室 キュリオステーション志木店のブログ




中学2年生の数学です 分からないので解き方教えて下さい Clear




指数関数 対数関数講座その2 指数から二次関数へ 高校数学の知識庫



1




関数の微分可能性4 指数関数e Xの導関数を微分の定義によって求める 身勝手な主張
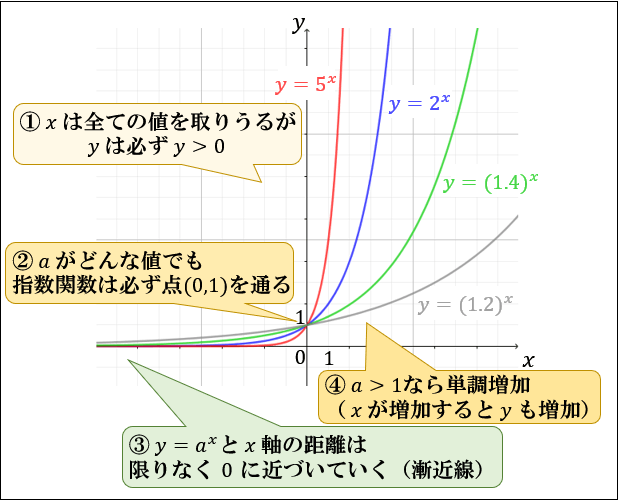



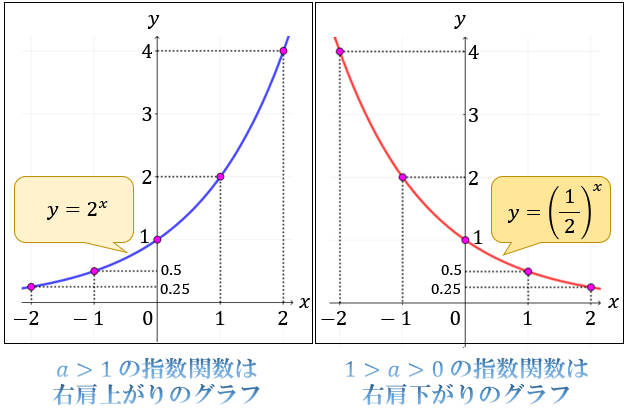
指数関数とは何か 指数と関数の意味からわかるグラフの仕組みとその性質 アタリマエ
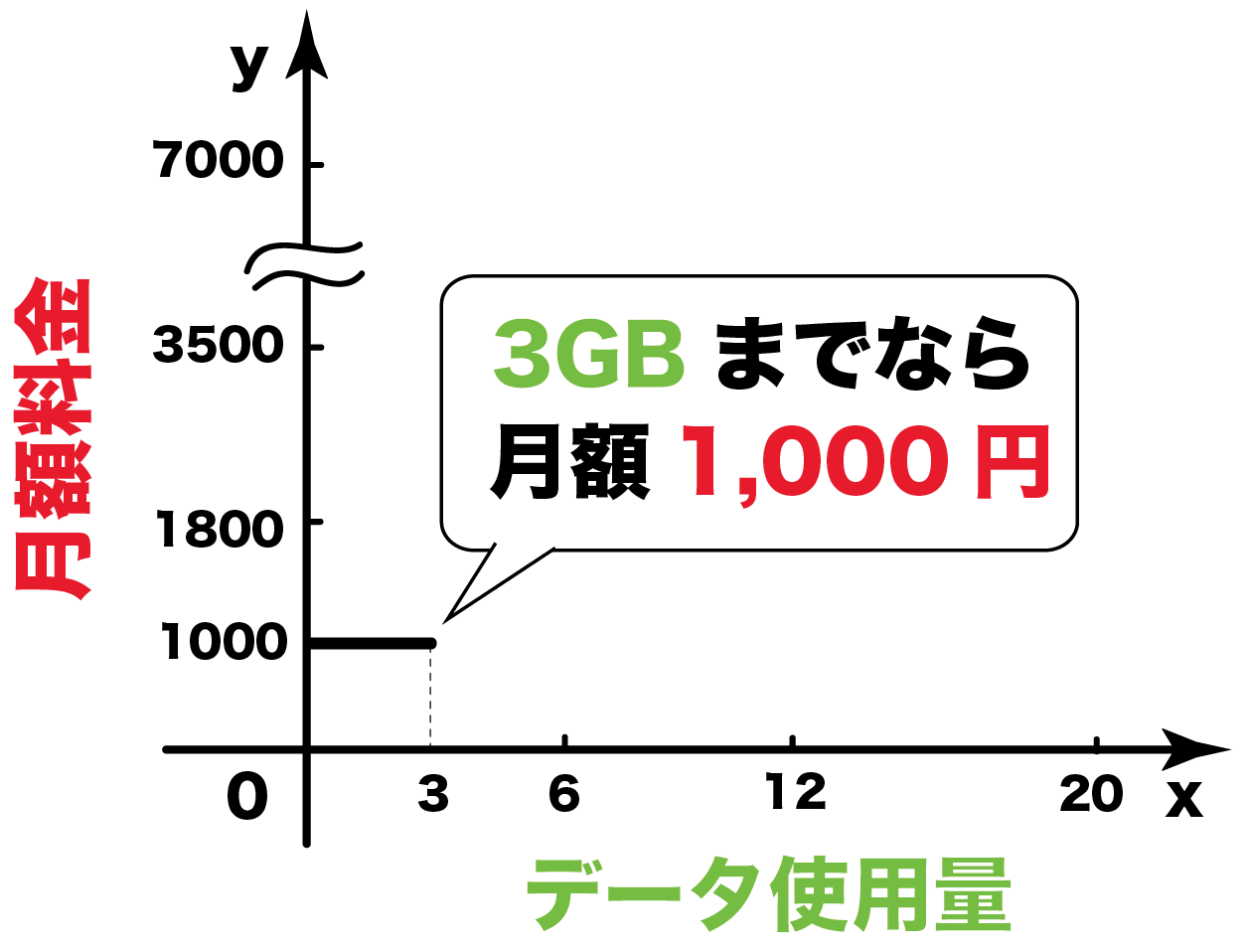



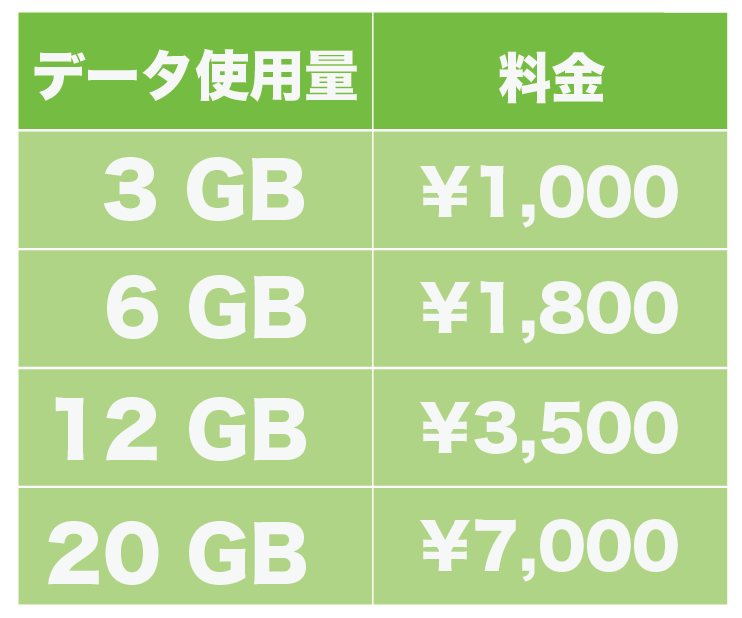
中3数学 いろいろな関数の問題の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく
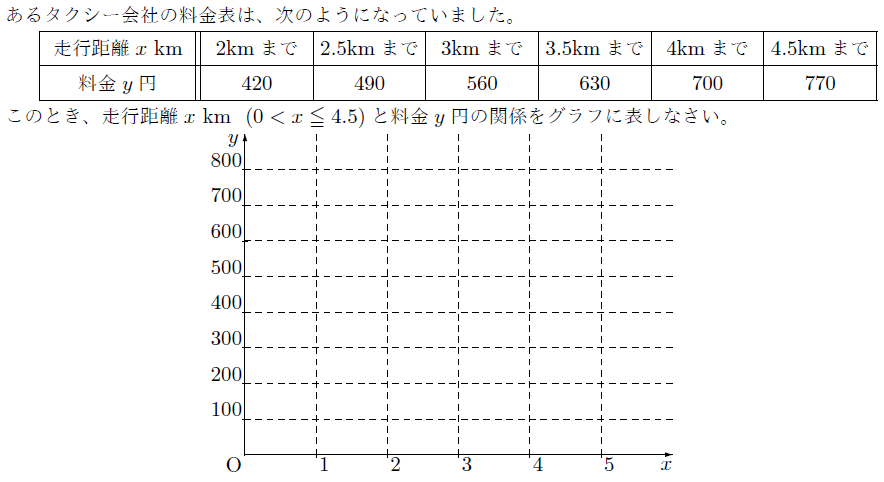



いろいろな関数 まなびの学園




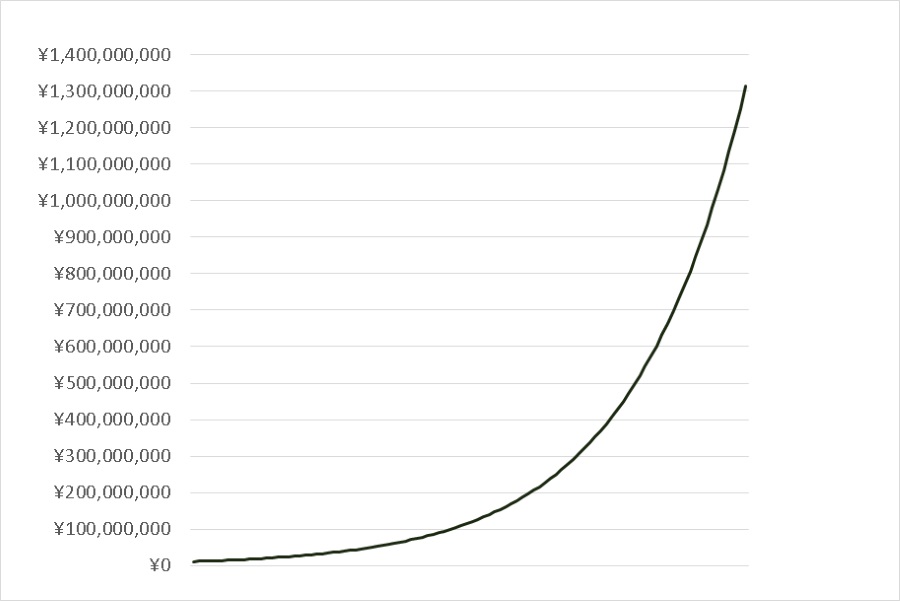
指数関数的増加 ってどういうこと 秀吉もびっくり 明石の塾なら中谷塾




いろいろな関数 無料で使える中学学習プリント




指数関数的減衰 Wikipedia
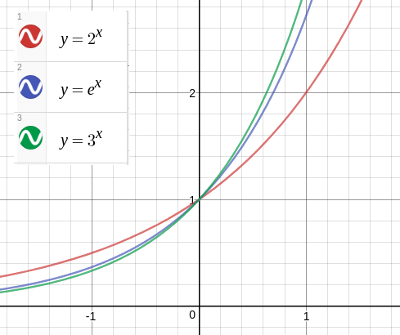



指数関数 初等数学 基礎からの数学入門



色々な関数の微分 べき関数編 高校数学の知識庫




標準 指数関数の逆関数 なかけんの数学ノート



数学2基礎 三角関数 指数関数 対数関数 演習コース 漫画 無料試し読みなら 電子書籍ストア ブックライブ




ボード ゼロ除算 のピン



数学2基礎 解説 例題コース 三角関数 指数関数 対数関数 最新刊 無料試し読みなら漫画 マンガ 電子書籍のコミックシーモア




ドイツ語で高校数学 いろいろな関数と微分 ふぁそらて 高校生 Note




指数関数とは何か 指数と関数の意味からわかるグラフの仕組みとその性質 アタリマエ




高等学校数学ii いろいろな関数 Wikibooks




中学3年生 数学 いろいろな事象と関数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




指数関数の意味と性質 グラフ
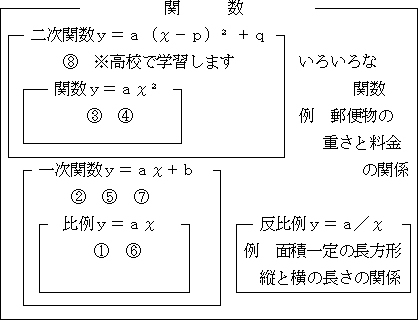



授業実践記録 数学
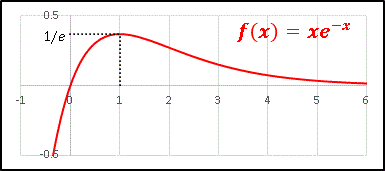



グラフ全体を下に押し下げて平たくなります




中学生 いろいろな関数の利用のノート一覧 Clear




いろいろな関数 無料で使える中学学習プリント




高等学校数学ii いろいろな関数 Wikibooks
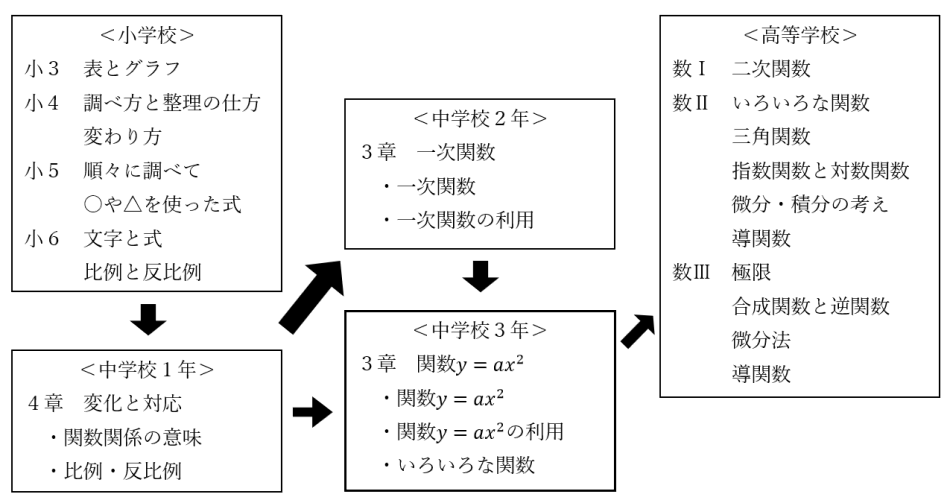



第2学年 一次関数 単元を貫く導入課題 授業実践記録 アーカイブ一覧 授業支援 サポート資料 数学 中学校 知が啓く 教科書の啓林館




初等関数概説 いろいろな関数 信 一松 本 通販 Amazon




指数関数とは何か 指数と関数の意味からわかるグラフの仕組みとその性質 アタリマエ



1




指数関数 対数関数
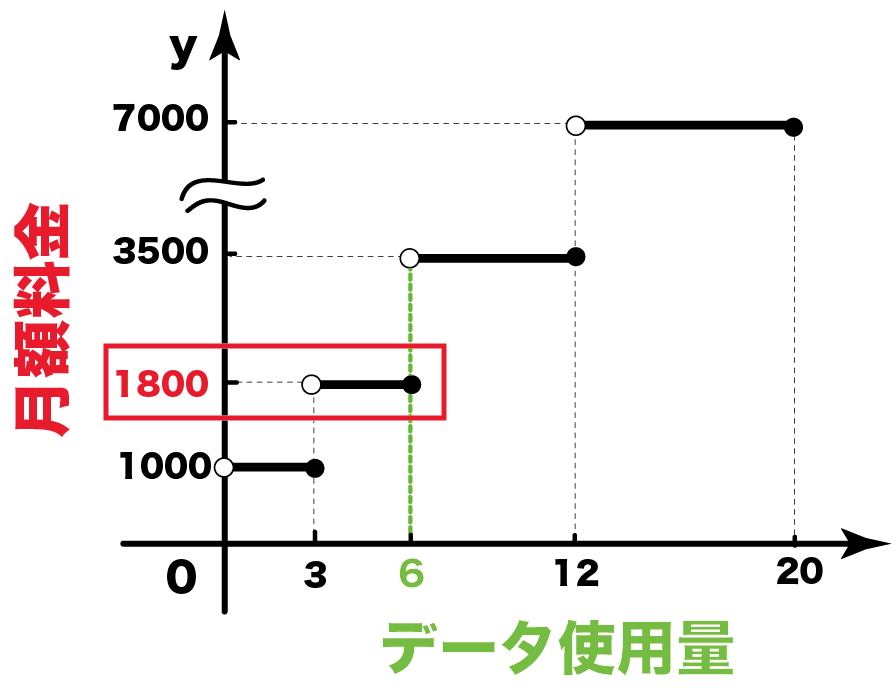



中3数学 いろいろな関数の問題の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく



Mathematicaに慣れよう 2
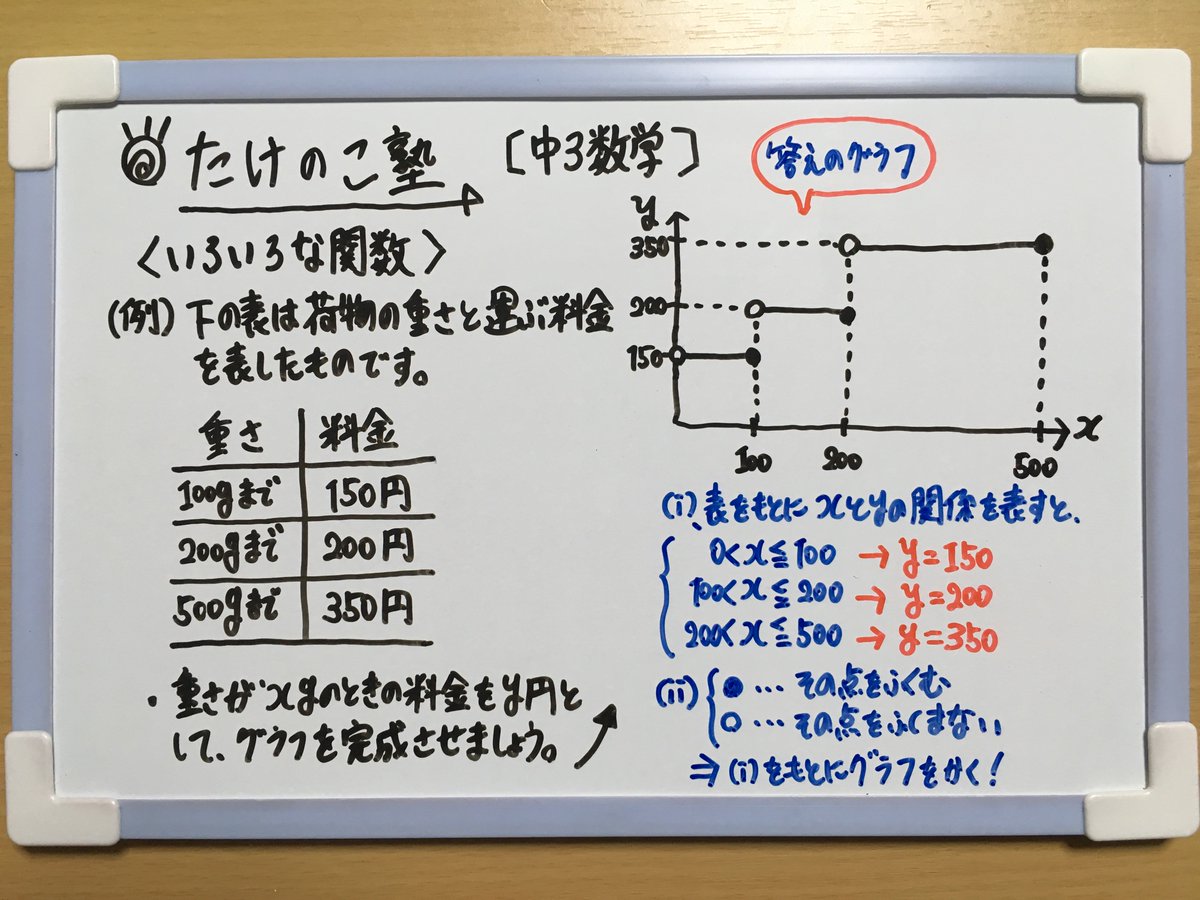



たけのこ塾 Auf Twitter 中3数学 今回は いろいろな関数 を作成しました いろいろな関数のグラフをかくとき はその点をふくむ はその点をふくまないことに注意しましょう 詳しくは画像の解説をご覧下さい 勉強垢 中3 数学 Youtube T




指数関数ものがたり 西郷 甲矢人 能美 十三 本 通販 Amazon



中3数学34 いろいろな関数 Youtube



いろいろな関数の積分




いろいろな関数の導関数 の問題のわからないを5分で解決 映像授業のtry It トライイット




指数関数のグラフの二通りの書き方 高校数学の美しい物語




いろいろな関数のグラフをgoogle先生に教えてもらおう 大学受験プラス



指数関数 対数関数の導関数




高等学校数学ii いろいろな関数 Wikibooks



指数関数のグラフと性質 これだけはサッと思い出したい 超重要な6つの性質 青春マスマティック



指数関数 続き




中学生 いろいろな関数の利用のノート一覧 Clear



世界一わかりやすい数学問題集中3 4章 二次関数



3




指数関数 Wikipedia



グラフを描くコツ



指数と対数の関係とは 変換公式やグラフの比較 計算問題 受験辞典




中3数学 いろいろな関数の問題の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




17 9 いろいろな関数 Youtube



指数関数とは何か 指数と関数の意味からわかるグラフの仕組みとその性質 アタリマエ



中3数学 いろいろな関数の問題の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




いろいろな関数の利用ー中3数学 Youtube




0s0s Dfracpi4leqdfracpi4 Descubre Como Resolverlo En Qanda




高校数学 関数の極限 指数関数と対数関数の極限 受験の月
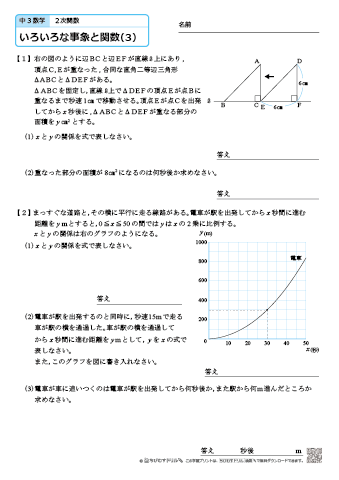



中学3年生 数学 いろいろな事象と関数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



指数関数 続き
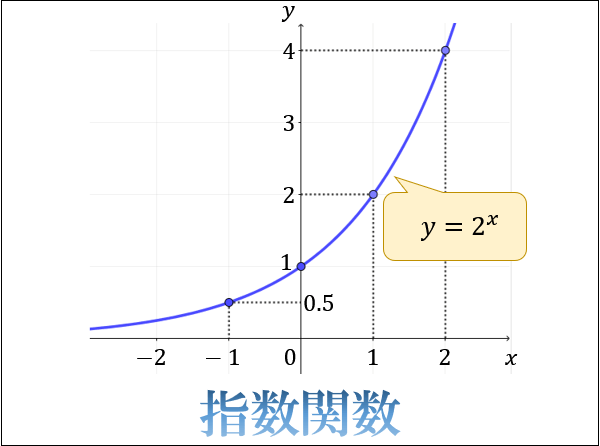



指数関数とは何か 指数と関数の意味からわかるグラフの仕組みとその性質 アタリマエ



いろいろな関数 対数




中3数学 いろいろな関数の問題の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




基本 指数関数のグラフ なかけんの数学ノート




高校数学 数 127 指数関数 グラフ編 Youtube




2 Descubre Como Resolverlo En Qanda




指数関数の定義 なぜ底が負のときは定義しないのか ダルいから 青春マスマティック




指数関数的増加 ってどういうこと 秀吉もびっくり 明石の塾なら中谷塾
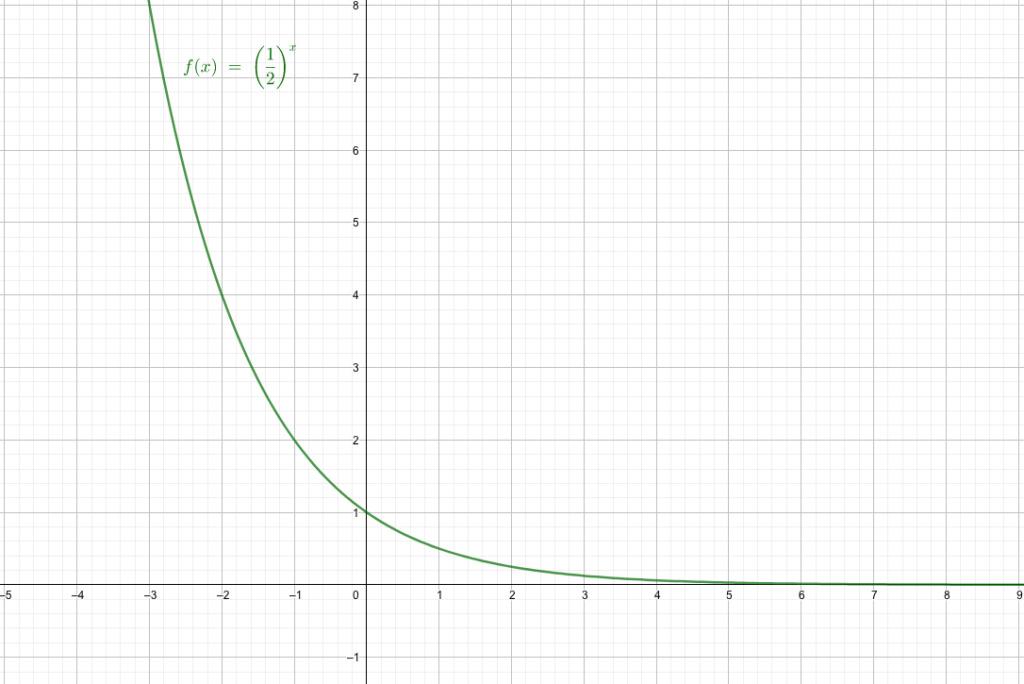



指数関数の定義 なぜ底が負のときは定義しないのか ダルいから 青春マスマティック
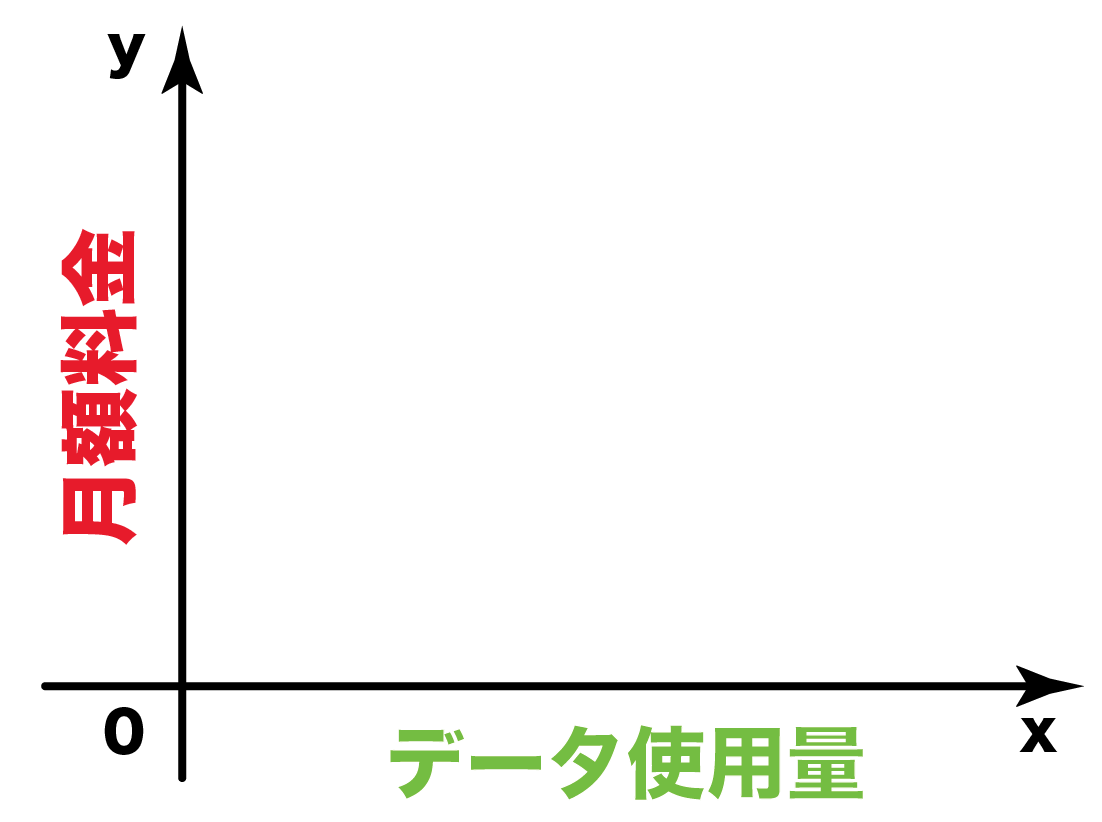



中3数学 いろいろな関数の問題の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく
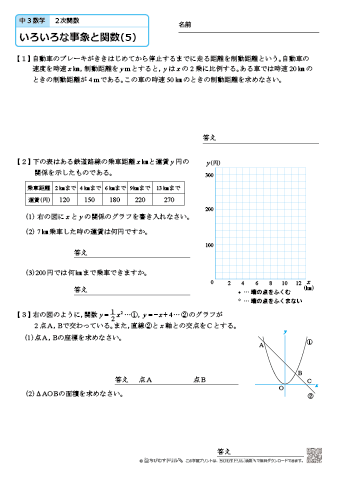



中学3年生 数学 いろいろな事象と関数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




いろんな関数 高校数学の美しい物語




指数関数 対数関数




池田洋介の いっきにわかる重要関数 2次関数 三角関数 指数関数 対数関数 数学が面白いほどわかるシリーズ 池田 洋介 本 通販 Amazon



3
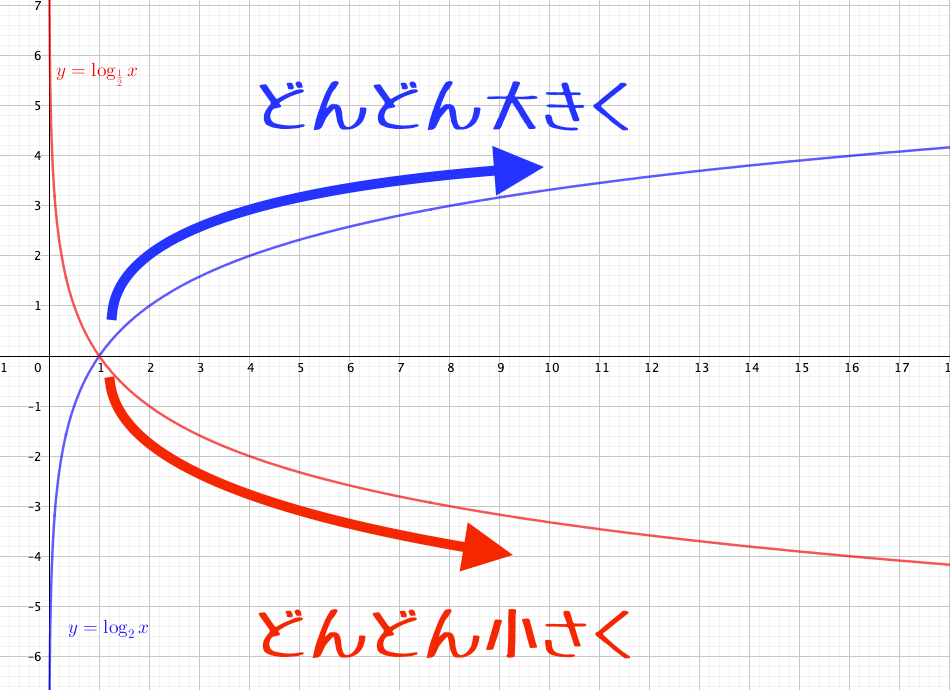



対数関数 攻略の6ポイント 値の増え方と指数関数に着目 青春マスマティック
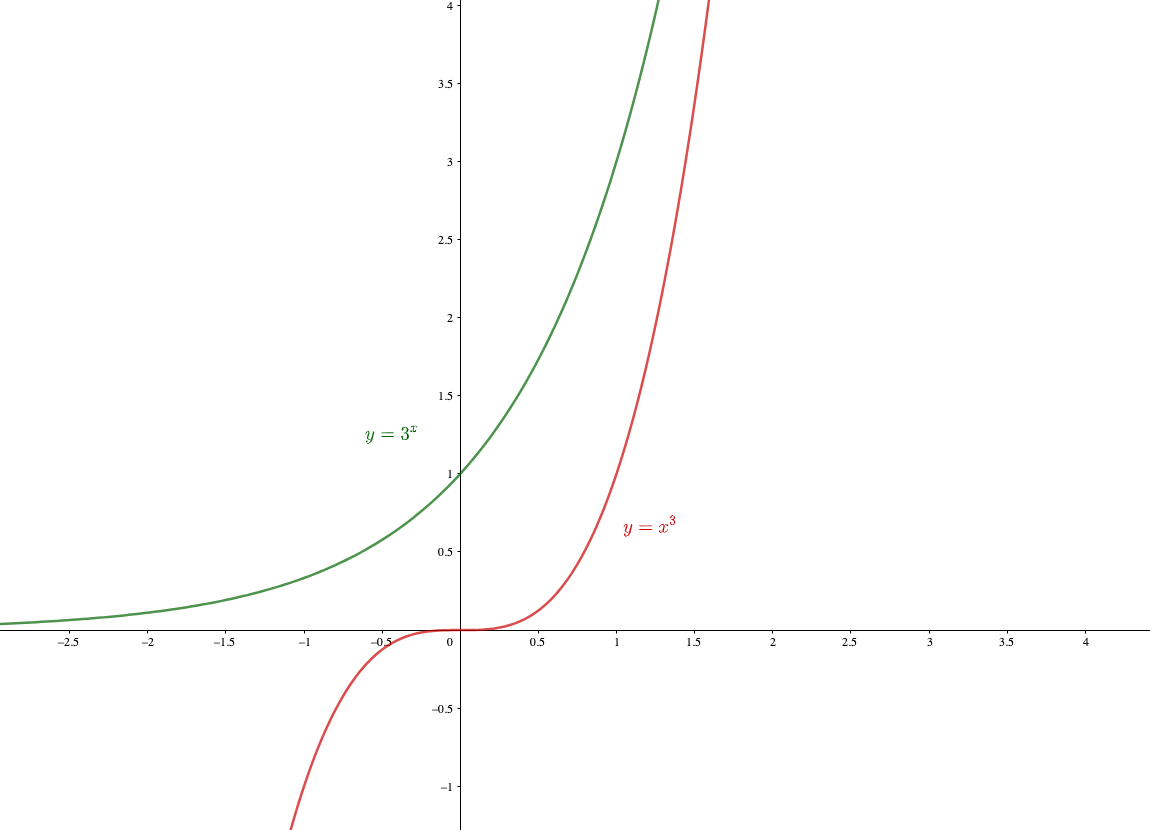



収束 発散の速さ 絶対に覚えておきたい極限の裏公式 見た瞬間に極限がヒラメク 青春マスマティック
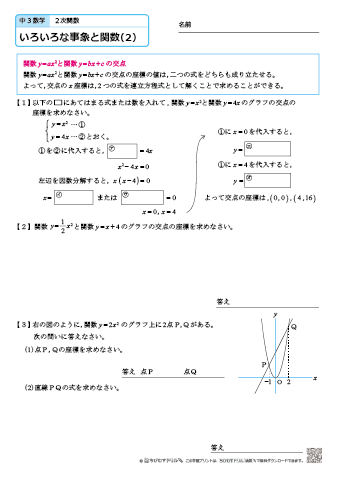



中学3年生 数学 いろいろな事象と関数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




世界一わかりやすい数学問題集中3 4章 二次関数
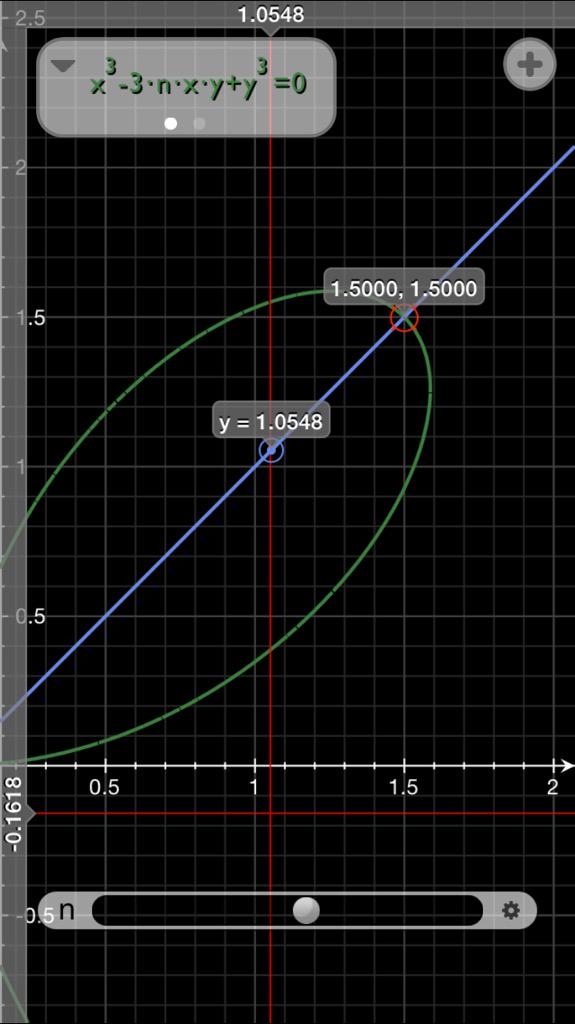



いろいろな関数
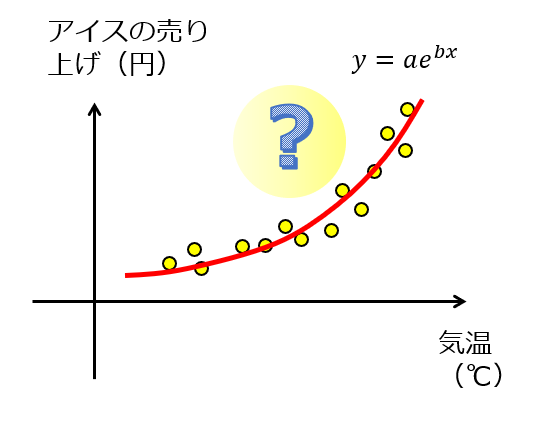



指数関数の意味 高校生からわかる近似曲線に指数関数を選ぶとき 宇宙に入ったカマキリ




指数関数をわかりやすく解説 グラフの書き方もマスターしよう 高校生向け受験応援メディア 受験のミカタ




指数関数とは何か 指数と関数の意味からわかるグラフの仕組みとその性質 アタリマエ
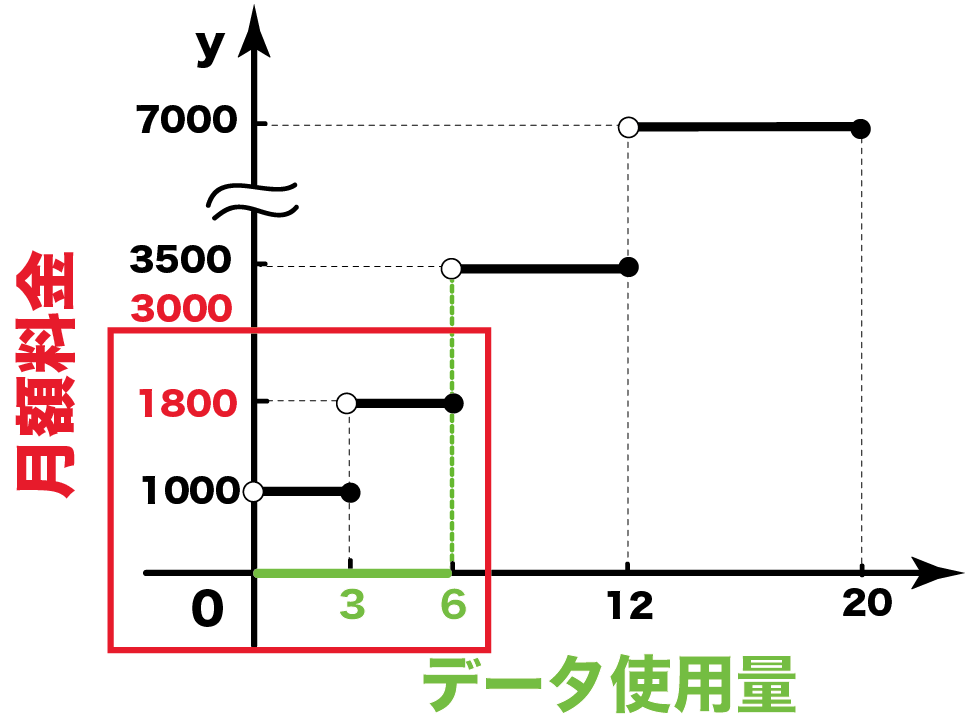



中3数学 いろいろな関数の問題の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




関数方程式を考える2 いろいろな関数方程式 身勝手な主張
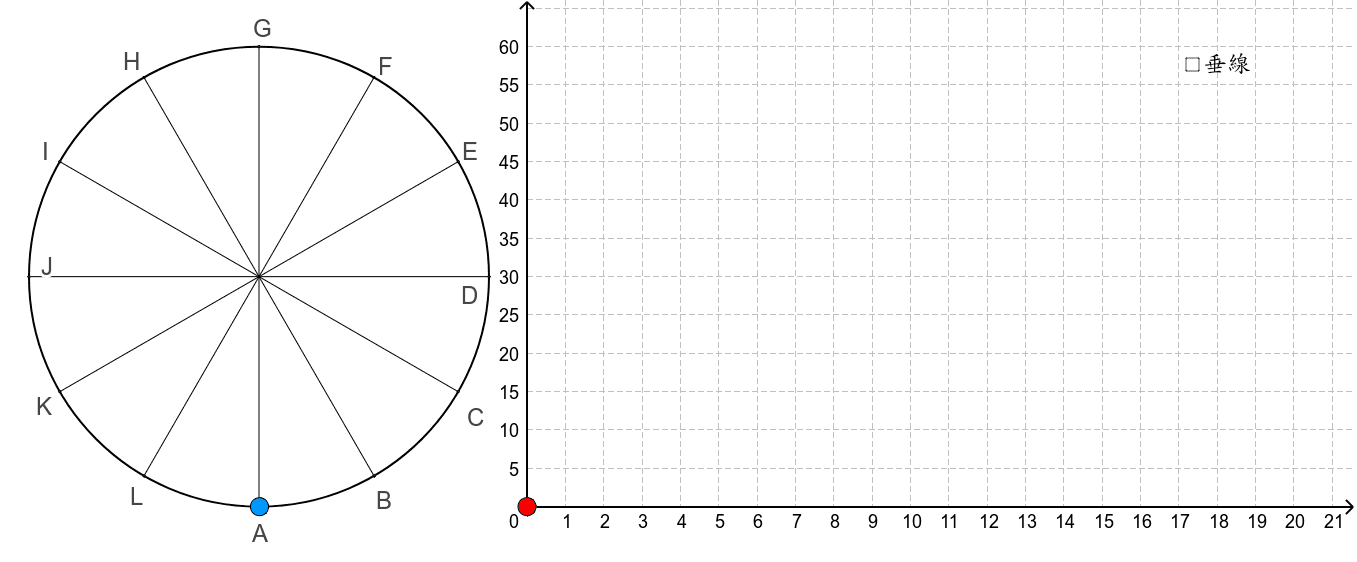



数学3 いろいろな関数 正弦曲線 Geogebra



Excelでグラフ



複素数の指数関数 対数関数 べき関数




指数関数の意味 高校生からわかる近似曲線に指数関数を選ぶとき 宇宙に入ったカマキリ



あなたの努力はどちらで報われる 対数的成長か 指数関数的成長か Ichiroyaのブログ




関数の単調性の証明 いろいろな方法で示してみよう 身勝手な主張




高等学校数学ii いろいろな関数 Wikibooks
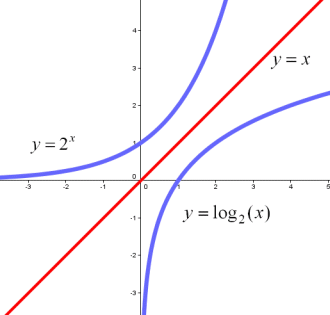



対数 対数関数と指数関数は 逆関数 大人が学び直す数学



0 件のコメント:
コメントを投稿