Simplify Answer Consider , As we know,(ab)2 = a2 b2 2ab 7 Question Simplify Answer √(32√2) = √ (√2)2 (1)2 2× √2×1 = √ (√2 – 1 )2 = √2 1 8 Question If a = 1, then find the value of a Answer Given , a = √2 1 = = 9 Question If x = 2 , find the value of x Free Online Scientific Notation Calculator Solve advanced problems in Physics, Mathematics and Engineering Math Expression Renderer, Plots, Unit Converter, Equation Solver, Complex Numbers, Calculation HistoryPlay this game to review Algebra II √98 5√2 Q The number under the radical sign or square root sign is called the _____
How To Simplify Math Frac 3 Sqrt8 Frac 1 Sqrt2 Math Quora
2 3 x 2 4 simplify
2 3 x 2 4 simplify- Class 9 Exercise 11 Number System (Multiple Choice Questions) Write the correct answer in each of the following Q1 Every rational number is A) a natural number B) an integer C) a real number D) a whole numberAnswer √2, when 32 is factored it becomes 2× 2× 2× 2× 2




Simplifying Square Root Expressions No Variables Video Khan Academy
SolutionShow Solution (√3 √2 ) 2 = ( √3 ) 2 ( √2 ) 2 2 x √3 x √2 = 3 2 2√6 = 5 2√6 Concept Concept of Real Numbers Report Error Is there an error in this question or solution? To simplify these, multiply both the numerator and denominator of the fraction by the conjugate of the denominator The conjugate of x √y is x √y The conjugate of x √y is x √y The conjugate of x a√y is x a√y As an example To simplify (2 √3) / (4 √5) multiply both the numerator and denominator by 4 √5Click here👆to get an answer to your question ️ Simplify ( 3 √(3)) (2 √(2))^2
Example 4 4 minutes example 4 simplify the square Example 4 (4 minutes) Example 4 Simplify the square root as much as possible √𝟐𝟖𝟖 = In this example, students may or may not recognize 2 as 144 × 2 The work below assumes that they do not Consider showing students the solution below, as well as this alternative solution √View Full Answer 3root2 multiply 4 root23 (4root 32root2)(3root24root3) 12rootroot6 364root6 hope this500 Surds & Indices Aptitude MCQ Live Quiz For IBPS Exam Quants Aptitude Multiple choice questions and answer practice test problems on Simplifying Roots With Values For all Bank IBPS PO SO CLERICAL Prelims & Mains July2621 by Careericons
Question 1 Simplify eg Question 2 Un a) f) b) g) c) h) d) i) e) j) √50 √80 g) √125 √0 √180 650 √0 1250 1125 3360simplify eg a) b) 17 c) d) i) e) j) f) h) 23 3√5 97 6√11 8√13 19√17 √19 23√23 29√29 99√31 √150= 5√6 1505√6= √ Examples ofSimplify Radical and Radical Operations STUDY Flashcards Learn Write Spell Test PLAY Match Gravity Created by Linzi_Bullard Terms in this set (60) 2√2 √8 2√3 √12 2√5 √ 6√3 2√23√3 √8 3√3505√5 * √ 2√22 √ 3√7 √63 2√7 √28 2√5 √ 2√11 √44 4√15 √60 3 9 Write a pair of irrational numbers whose difference is irrational Answer √3 2 and √2 – 3 are two irrational numbers whose difference is irrational (√3 2) – (√2 – 3) = √3 – √2 2 3 = √3 – √2 5 which is irrational 10Write a pair of irrational numbers whose difference is rational Answer



1




Simplify Root 4 Root 3 X 2 And Express The Result In The Exponential Form Of X Youtube
Simplify √10 x √5 1/√2 Simplify 4 ÷ 2√2 10√2 Simplify √0 √6 2√2 The conjugate of √6 2√2 3 √27/√33, 1, 0, 1, 3, 5 Examples of Integers Rational Numbers√ 3 2 √ 2 2 √ 1 2 √ 0 2 Simplify the Arithmetic θ(radians) 0 √ 3 2 √ 2 2 1 2 0 selected by vikash gupta Best answer (i) (3 √3) (2 √2) We need to apply distributive law to find value of (3 √3) (2 √2) (3 √3) (2 √2) = 3 (2 √2) (3 (2 √2) = 6 3√2 2√3 √6 Therefore, on simplifying (3 √3) (2 √2) we get 6 3√2 2√3 √6 (ii) (3 √3) (3 √3)
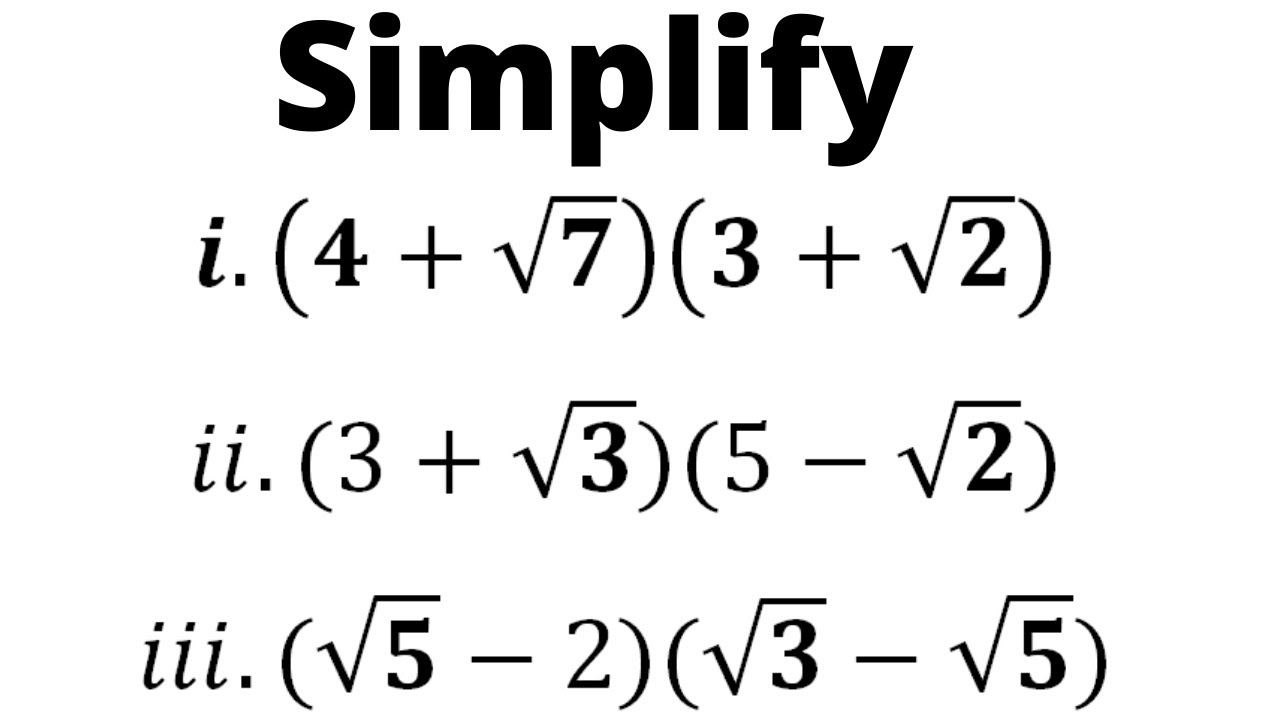



Simplify I 4 Root 7 3 Root 2 Ii 3 Root 3 5 Root 2 Iii Root 5 2 Root 3 Root 5 Youtube



Simplify Whole Root 3 2 Root 2 Brainly In
Simplify Answer √(32√2) = √ (√2) 2 (1) 2 2× √2×1 = √ (√2 – 1 ) 2 = √2 1 Question 15 If a = 1, then find the value of a Answer Given , a = √2 1 = = Question 16 The simplest rationalising factor of is A 5 B 3C D Answer Simplest rationalizing factor of Simplify √(32√2) √(32√2) =√(32*1141) =√() =√52 =2298 =23 By simplifying the given tangent expression, it results in tan (239°) Example 9 Simplifying a Tangent Expression to a Single Term Example 10 Finding the Exact Values Using the Sum or Difference Identities in Trigonometry (√3 / 2) (√2 / 2)




Simplifying Square Root Expressions No Variables Video Khan Academy




Simplify 3 3 2 2 Brainly In
To clear their doubts instantly, students can refer to Frank Solutions for Class 9 Maths Chapter 1 Irrational Numbers PDF, from the links which are given below Chapter 1 of Frank Solutions has problems based on irrational numbers A real number which cannot be written in a simple fraction is known as an irrational numberRadical Expressions & Functions 2 5 What is the smallest term that could be multiplied to √32 to create a perfect square?Solution (3 √3) (2 √2) = (3 × 2) (3 × √2) (√3 × 2) √3× √2 = 6 3√2 2√3 √6 (ii) (3 √?) (3 – √?) Solution (3 √3) (3 –√3) = 3²− (√3)² (a b)(a – b) = a² b² =9 – 3




Simplifying Square Root Expressions No Variables Video Khan Academy




2 3 2 3 2 3 2 3 3 1 3 1 Simplify Brainly In
A) Always an integer b) Always a25 Questions Show answers Q The perimeter of a rectangle is √5 If the length of the rectangle is 8√5, find the width Q The area of a rectangle is 15√6 If the length of the rectangle is 3√2, the width is QSimplify Radicals Product Property of Radicals For any real numbers a and b, and any integer n > 1 1 if n is even and a and b are both nonnegative, then 𝑛√ √= 𝑛√ ⋅ 𝑛 2 if n is odd, then √𝑛 √= 𝑛 ⋅√𝑛 To simplify a square root, follow these steps 1




Simplify Squareroot 128a 4 B 6 E 8 3 Squareroot Chegg Com




Add 3 2 7 3 And 2 5 3 Rational Numbers Video Teachoo
Simplify 1 2 √8=2√2so 1÷√√2=1÷2√23√2=1÷√2so a Simplify 1/ 2 Please scroll down to see the correct answer and solution guideSimplify by Rationalising the Denominator in the Following 3 − √ 3 2 √ 2 CISCE ICSE Class 9 Question Papers 10 Textbook Solutions Important Solutions 5 Question Bank Solutions Concept Notes & Videos 258 Syllabus Advertisement Remove all ads Simplify by Rationalising the Denominator in the Following 3 − √ 3 2 how to simplify (4 root 3 2 root 2) (3 root 2 4 root 3) Share with your friends 2 √2)(4 √3 3 √2) 4 √3 * 4 √3 4 √3 * 3 √2 2 √2*4 √3 2 √2*3 √2 48 12 √6 8 √6 12 36 4 √6 10 ;




Ex 1 5 2 Simplify Each I 3 Root 3 2 Root 2 Ex 1 5



Simplifying By Rationalising The Denominator 1 3 2 5 Studyrankersonline
3 Simplify each radical To eliminate radicals from a denominator or fractions from a radicand, multiply the numerator and denominator by a quantity so that the radicand has an exact root Simplify 3 √6a5b7 3 √16a5b7 3= √ (2)3 2 3 a a2 (b2) b = 2ab2 3 √ 2a b 2 Simplify √ 8x 3 45y5 √ 8x 3 45y5 = √ 8x 45y5 Quotient Property = − After rationalising the denominator of 7/(3√3 2√2), we get the denominator as (a) 13 (b) 19 (c) 5 (d) 35 asked in Mathematics by RahulSingh (1 Simplifying Surds Answers √15 √10x √3 √x 5 √2x √5 √5 x √5 xx√3 √2 5 x √6 Ans 5√6 Example Method 1 150 √25 x √6 5 x √6 Ans 5√6 Example Method 2 Decompose into prime factors Rearrange to collect like terms Simplify Find a square factor Simplify Question 1 Simplify eg Question 2 Un a) f) b) g) c) h) d




Simplify 3 2 2 Evaluate 53 10 6 Cambridge Interview Maths Questions Sqrt 3 2 Sqrt 2 Youtube




Simplify Each Of The Following Expressions I 3 Sqrt 3 2 Sqrt 2 Ii 3 Sqrt 3 3 Sqr Youtube
To represent √93 on the number line, follow the following steps, Step 1 Draw a 93 units long line segment, name the line as AB Step 2 Extend AB to C such that BC=1 unit Step 3 Now, AC = 103 units Let the centre of AC be O Step 4 Draw a semicircle with radius OC and centre O Step 5 Draw a BD perpendicular to AC at point B which2√32√2 √ =9√2 √ Numerator and Denominator Simplify a 22 𝑛1161−𝑛 4𝑛1 =2 3(2𝑛1)24(1−𝑛) 22(𝑛1) √ √ =26 𝑛3 4 −2 √ =25 or 32 √ Base 2 23 Undefined √ a 9 Q14 Simplify (i) 7 2/37 1/5 (ii) 10 1/2 /10 1/4 Solution (i) 7 2/37 1/5 Bases are equal, so add the powers 7 (2/3 1/5) = 7 (10 3)/15 = 7 13/15 (ii) 10 1/2 /10 1/4 Bases are equal, so subtract the powers = 10 (1/2 – 1/4) = 10 1/4 Q15 What is the product of a rational and an irrational number?




Simplify 3 3 2




3 Ways To Simplify A Square Root Wikihow
(10 x 10^3) (2 x 10^6) Simplify the problem and express the answer in scientific notation Show your work Please help!!!Multiply top and bottom by (√3–2) so top will now be 6 (√3–2) which expands to 6√3–12 bottom will now be (√32) (√3–2) which expands to √3√3 2√3–2√3–4 which simplifies to 1 So (top)/ (bottom) will be (6√3–12)/ (1) which is 12–6√3 (Ans) 13K views= (√2/2) (√3/2) (√2/2) (1/2) = √6 √2 /4 3) tan(ab) Example 3 Calculate tan75° 4) cot(ab) Example 4 Calculate cot75° B) The Trig Ratios of (ab) If in the formulas for (ab), b is replaced with b, the formulas for the difference (ab) will simply result 1) sin(ab)




Multiplying And Dividing Radical Expressions




Simplify 3 2 6 3 4 3 6 2 Brainly In
Simplify the following (1) (3√2) 2 (2) 2√3 × 4√3 (3) 3√2 √8 (4) 2√3 × 3√5 (5) (2√5) 2 (6) 5√2 7√2 (7) (√3) 4 (8) √3 × √5 × √15 (9) Write √48 in simplest radical form (10) Write √75 in simplest radical form Solution Ex15, 2 Simplify each of the following expressions (i) (3 √3) (2 √2) (3 √3) (2 √2) = 3(2 √2) √3(2 √2) = 3 × 2 3 × √2 √3 × 22 Simplifying Square Roots Lessons on simplifying radicals, as well as performing operations (rationalizing denominators) can be found in EngageNY Grade 8 Module 7, lesson 4, as well as in the Geometry Module 2, lessons 22 and 23 3
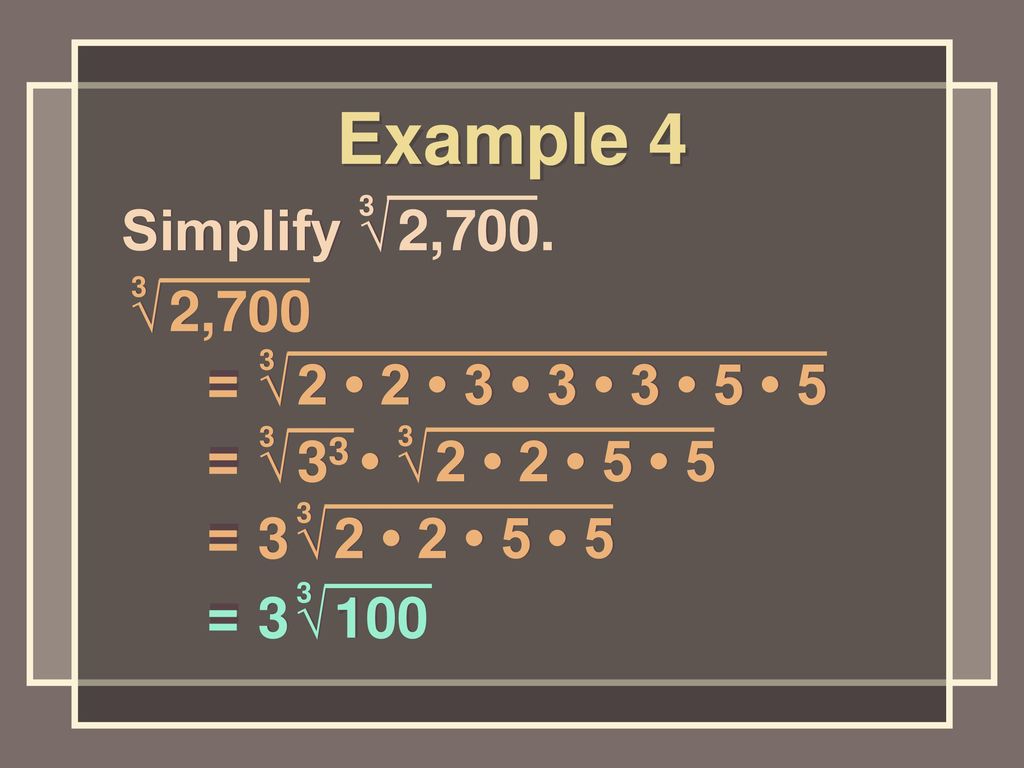



Exercise Simplify 22 Ppt Download




3 Ways To Simplify A Square Root Wikihow
NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 14 Ex 14 Class 9 Maths Question 1 Visualise 3765 on the number line, using successive magnification Solution 3765 lies between 3 and 4 Ex 14 Class 9 Maths Question 2 Visualise 4 on the number line, upto 4In this case all you need to do is rationalize the radical in the denominator (ex 2/(√7)=(2√7)/7) A final answer can't have a square root in the denominator This will give you the exact answer, which is what I assume you mean by "simplify" ((√3)/3)(√2)(√5) The estimated answer ((√3)/3)(√2)(√5)≈(()/3)(√2)(√5)Expand and simplify where possible a) 3 (8 − √ 5) b) √ 3 (√ 6 − √ 3) c) 8 √ 2 (2 √ 8 3 √ 12) d) (√ 2 5) (√ 2 5) e) (√ 3 2 √ 2) (5 5 √ 2) f) (1 √ 5) (1 − √ 5) g) (4 − 3 √ 7) (√ 7 1) 7 Solve by factoring a) x 2 8 x 12 = 0 b) x 2 = 2 x c) 3 x 2 28 x =− 9 d) 16 x 2 − 1 = 0 e) 6 x 2




Simplify 4 2 2 8 3 2 Brainly In




Simplify Math Dfrac 4 Sqrt 3 2 Sqrt 2 Dfrac 30 4 Sqrt 3 Sqrt 18 Dfrac Sqrt 18 3 2 Sqrt 3 Math Quora
Rationalising Rationalising denominator of irrational number Add (3√27√3) and (√2−5√3) Divide 5√11 by 3√33 Multiply 2√15 by 7√5 Simplify (√5√7)^2To simplify (or divide) a fraction with a square root radical and another term in the denominator, you must multiply both the numerator and the denominator by the conjugate of the denominator Then simplify 36 √32√2 3√22√3Click here👆to get an answer to your question ️ Simplify the following expression ( 3 √(3)) ( 2 √(2))




Cp Alg 2 5 6 Radical Expressions




How To Solve 1 1 2 2 3 Quora
Simplify (3√3) (2√2) Get the answers you need, now!




Rd Sharma Class 9th Solutions Chapter 3 Rationalisation
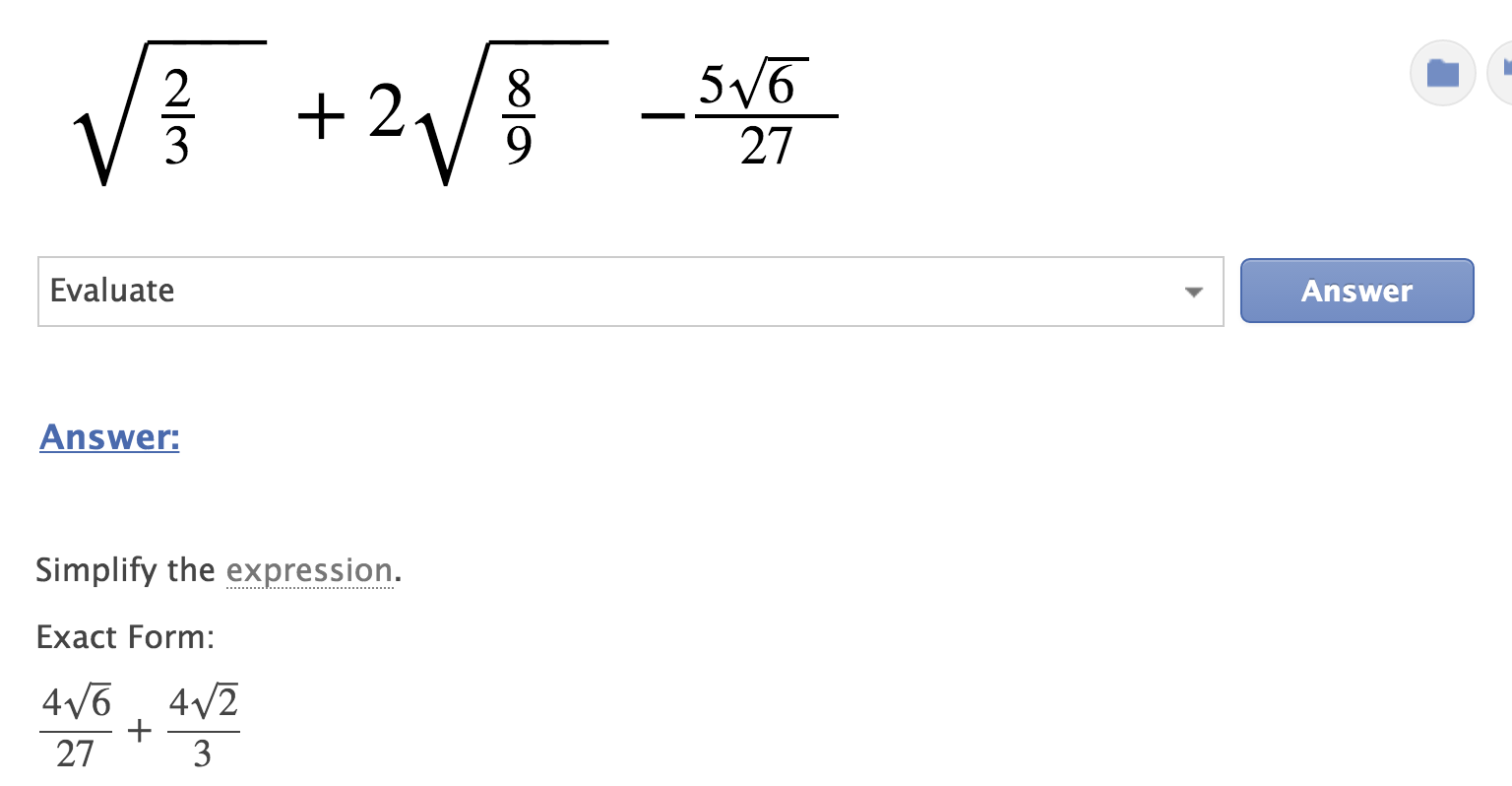



Squareroot 2 3 2 Squareroot 8 9 5 Squareroot 6 27 Chegg Com




How To Multiply Square Roots 8 Steps With Pictures Wikihow




Simplify 3 5 3 2 5 3 Youtube




Simplify And Rationalise The Denominator Of 6 4 2 6 4 2




Ex 1 6 3 Simplify I 2 2 3 2 1 5 Ii 1 33 7 Ex 1 6



Simplify 7 3 10 3 2 5 6 5 3 2 15 3 2 Sarthaks Econnect Largest Online Education Community



Rationalize The Denominator And Simplify I 3 2 3 2 Ii 5 2 3 7 4 3 Sarthaks Econnect Largest Online Education Community




Simplify 3 5 5 2 4 5 3 2 With Video Teachoo Rationalising




Simplifying Taylor Series For The Function Sqrt 2 X About X 3 Mathematics Stack Exchange




Strategy And Trick To Find Square Root Of 8 2 15 Radical Expressions Youtube




Multiplying And Dividing Radical Expressions




Simplify 6 2 3 6 6 3 2 4 3 6 2 Brainly In




Simplify The Following Expressions I 5 Sqrt 7 2 Sqrt 5 Ii 5 Sqrt 5 5 Sqrt 5 Iii Sqrt 3 Sqrt 7 2 Iv Sqrt 11 Sqrt 7 Sqrt 11 Sqrt 7




Multiplying And Dividing Radical Expressions




Simplify 6 2 3 2 Brainly In



Simplifying By Rationalising The Denominator 3 5 3 2 5 3 Studyrankersonline



Simplify 2 45 3 2 5 And Clear Whether It Is Rational Or Irrational Number Sarthaks Econnect Largest Online Education Community




Plz Simplify 3 5 5 2 4 5 3 2 Brainly In




Multiplying And Dividing Radical Expressions




Square Root Of 2 3 Root 2 Maths Number Systems Meritnation Com




After Rationalizing The Denominator Of 2 3 5 2 2 3 3 And Simplifying We Get A 3 15 B 10 4 6 19 Then The Value Of A B Is




Rd Sharma Class 9 Solutions Maths Chapter 3 Rationalisation



What Is The Answer Of Simplify 7 3 5 3 5 7 3 5 3 5 Quora
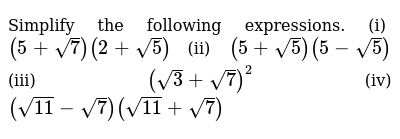



Simplify The Following Expressions I 5 Sqrt 7 2 Sqrt 5 Ii 5 Sqrt 5 5 Sqrt 5 Iii Sqrt 3 Sqrt 7 2 Iv Sqrt 11 Sqrt 7 Sqrt 11 Sqrt 7




How To Solve Surds 2 Four Essential Surd Techniques Suresolv




Question 1 1 1 Simplify The Following Expressions Gauthmath




How To Add And Subtract Square Roots 9 Steps With Pictures




2 Sqrt 3 2 Sqrt 3 2 Sqrt 3 2 Sqrt 3 Sqrt 3 1 Sqr



Solved Multiply And Simplify 3 2 Square Root 5 3 2 Square Root 5 Sorry No Square Root Button Course Hero




Simplify By Rationalising The Denominator 7 Root 3 5 Root 2 Root 48 Root 18 Youtube




Simplify 3 3 2 27 7 3 Brainly In
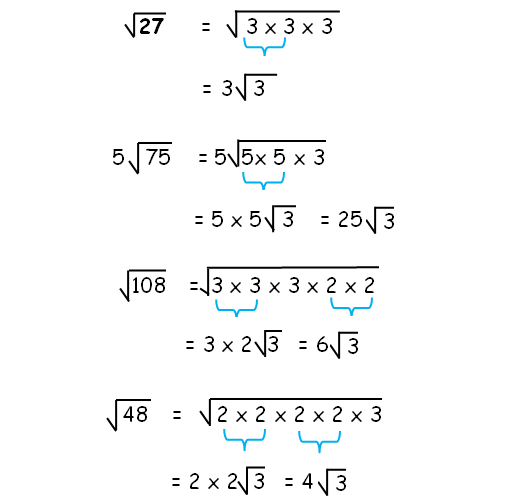



Simplify Radical Expressions




Simplifying Square Root Expressions Video Khan Academy




Simplify 7 3 10 3 2 5 6 5 3 2 15 3 2 V




Ex 1 6 3 Simplify I 2 2 3 2 1 5 Ii 1 33 7 Ex 1 6



Simplify 4 3 3 48 5 2 1 3 Sarthaks Econnect Largest Online Education Community




Simplify 2 5 3 1 3 2 3 5 2



Simplify I 4 7 147 3 8 192 1 5 75 Ii 5 3 2 27 1 3 Iii 216 5 6 294 3 6 Sarthaks Econnect Largest Online Education Community



Simplify 2 3 2 3 2 3 2 3 Studyrankersonline




What Is The Solution Of 2 3 2 3 Quora




Ex 1 5 2 Simplify Each I 3 Root 3 2 Root 2 Ex 1 5



Q Tbn And9gctrunxjecpqbdzj9zqrqco87xea9aho7zc7d99tsrnydmdcfq1o Usqp Cau




Simplify 7 5 3 2 2 5 4 2 Brainly In




Simplify 1 2 3 2 2 Tex Pleasesimplify Tex Brainly In




Simplify 5 7 2 With Video Chapter 1 Class 9 Maths Teachoo




Ex 13 1 7 Simplify I 4 3 Ii 3 X 2 3 Iii 3 2 X



Simplify 7 3 10 3 2 5 6 5 3 2 15 3 2 Studyrankersonline



How To Simplify Math Frac 3 Sqrt8 Frac 1 Sqrt2 Math Quora




Surds Objectives Grade A Rationalise The Denominator Of A Surd Such As Grade A Simplify Surds Such As Write In The Form Ppt Download




A Cambridge Interview Problem Sqrt 3 2sqrt 2 Youtube



Simplifying By Rationalising The Denominator 6 4 2 6 4 2 Studyrankersonline




Simplify The Product 4 3 3 2 4 3 3 2 Brainly In




Chapter 7 Radicals Radical Functions And Rational Exponents Ppt Video Online Download



What Is The Square Root Of 5 2 Root 6 Quora



Simplifying By Rationalising The Denominator 4 2 3 7 Studyrankersonline




Example 16 Simplify The Following Expressions Class 9



Q Tbn And9gcqt8xcypqw0rmdh64vbuopwz1cxhnbqpt756epqa I9o2cblok Usqp Cau




Simplify 3 5 5 2 4 5 3 2 Brainly In




Simplify Each Of The Following Expressions I 3 3 2 2 Ii 3 3 3 3 Iii 5 2 Brainly In




Simplify 1 3 11 3 11 2 3 5 3 5 3 3 3 24 5 3 25 5 7 2 5 6 5 2 2 3 Youtube



Simplify I 3 2 2 3 3 2 2 3 12 3 2 Ii 5 3 5 3 5 3 5 3 Sarthaks Econnect Largest Online Education Community




Evaluate Root 3 2root2 Evaluate Root 3 Plus 2 Root 2 Sqrt 3 2 Sqrt2 Youtube



1




Example 16 Simplify The Following Expressions Class 9
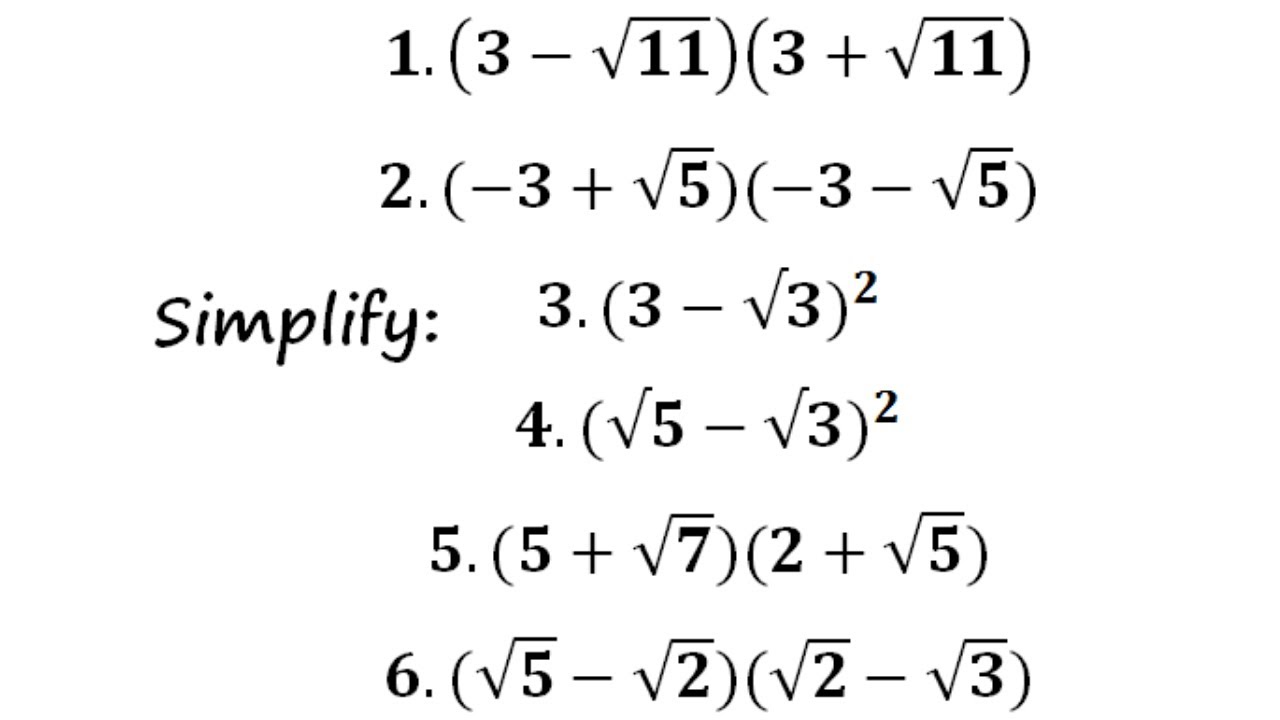



Simplify 1 3 11 3 11 2 3 5 3 5 3 3 3 24 5 3 25 5 7 2 5 6 5 2 2 3 Youtube




3 3 2 2 Dronstudy Questions




How Do You Simplify Frac 5 Sqrt 3 3 Sqrt 2 Sqrt 3 Sqrt 2 Socratic
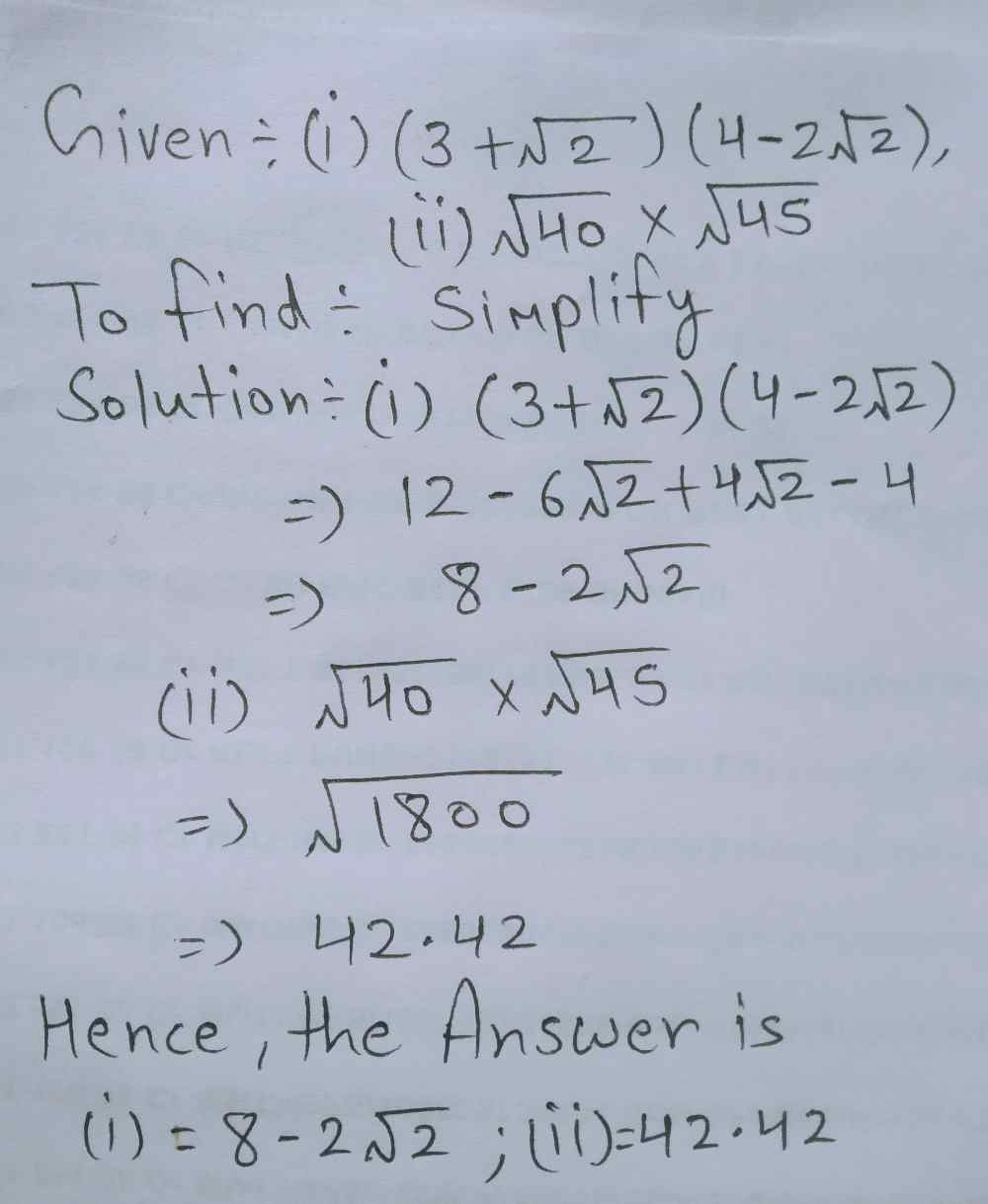



B Simplify The Expressions I 3 Square Root Of 2 Gauthmath




3 Ways To Simplify A Square Root Wikihow




Example 12 Simplify I 12 4 X 9 3 X 4 6 3 X 8 2 X 27 Ii 2 3




Simplify 1 3 2 2 5 3 3 2 5 Brainly In




Rationalise The Denominator And Simplify 1 2 3 2 2 Brainly In




Simplify 3 2 6 3 2 3 6 2 4 3 6 2 Brainly In




Simplify 1 1 2 1 2 3 1 3 4 Brainly In




Rd Sharma Class 9 Solutions Maths Chapter 3 Rationalisation



How To Simplify 2 3 6 3 3 27 Quora




Multiplying And Dividing Radical Expressions




Simplify 3 18 3 12 2 27 Youtube



Simplify 3 5 5 2 4 5 3 2 Brainly In



0 件のコメント:
コメントを投稿